|
Poincare disk model of hyperbolic plane.
Geodesics in this model are segments of circles orthogonal to the unit circle (circle at infinity).
The model is conformal - the angles between intersecting geodesics are equal to the euclidean angles
between the tangent lines of the circle.
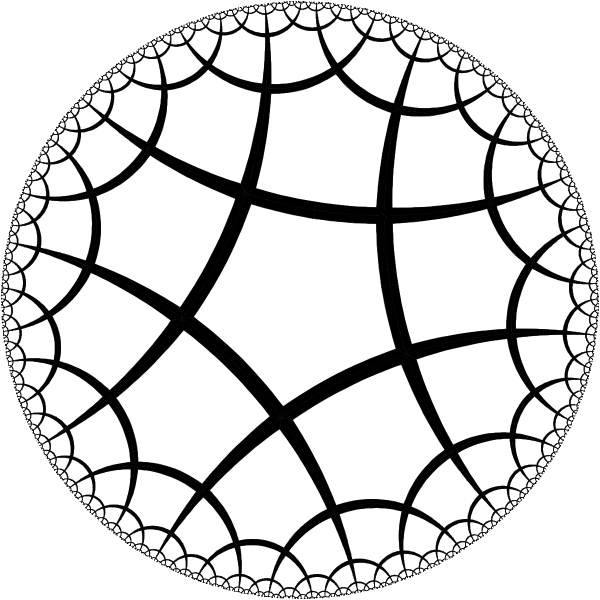
To visualize the hyperbolic geometry we will be using this tiling with right angled regular pentagons. It is analog of simple square tiling of the euclidean plane. |
|
By moving the center of a pentagon into the center of Poincare circle we can see that pentagons are actually regular. |
|
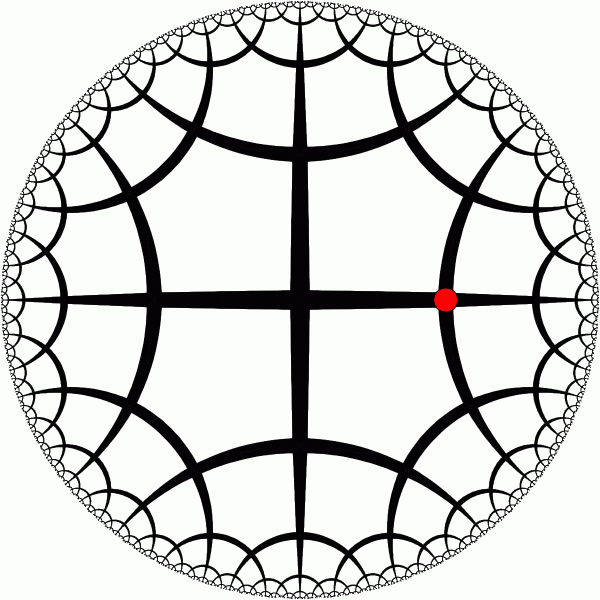
Hyperbolic plane has isometries similar to the isometries of the euclidean plane.
Here we have rotation around symmetry axis of 4th order. [animation] |
|
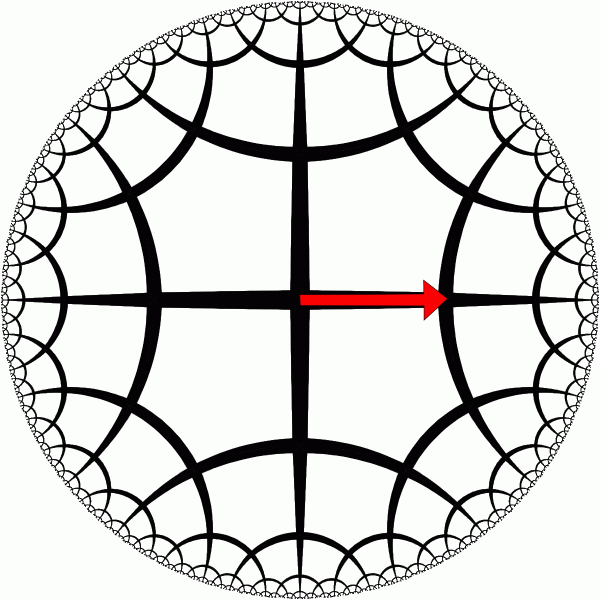
Hyperbolic translation along X-axis. [animation] |
|
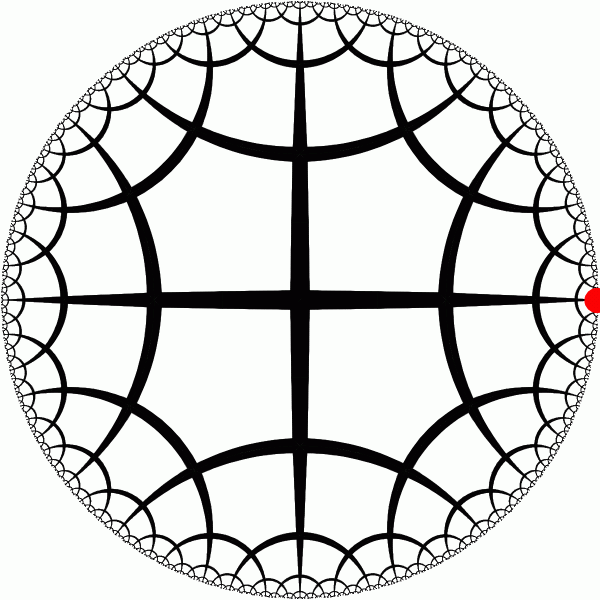
This ideal rotation around the point at infinity has no analog in the euclidean geometry.
[animation] |
|
Upper half plane model is another standard model of the hyperbolic geometry. Geodesics are half circles orthogonal to the horizontal axis. The model is also conformal. |
m
|
This is a rotation of the hyperbolic plane around an axis of 4th order
[animation] |
|
This is translation of the hyperbolic plane in Y direction in the upper half plane model
[animation] |
|
Ideal Rotation around a point at infinity
[animation] |
|
|
Isometries of the disk model and the upper half plane models are particular cases of the Moebius transformation
- general linear fractional transformation of the complex plane $C$:
`M(z) = (az+b)/(cz+d)` |
|
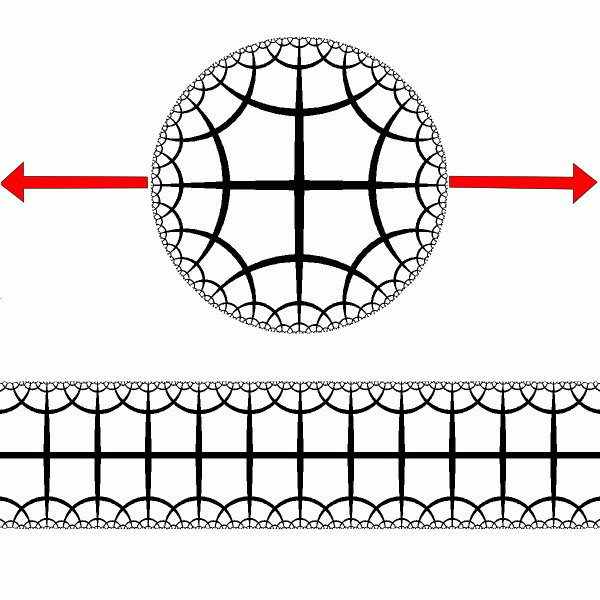
Band model of the hyperbolic plane is obtained by applying to the disk model a special conformal
map of the complex plane:
`w =(2/\pi)tanh\^-1(z); z, w \in CC, |Im(w)| < 1, |z| < 1` Particular points are mapped as follows: `[[1,\to,+\infty],[-1,\to,-\infty],[i,\to,i],[-i,\to,-i]]` The band model is conformal, because it is obtained from disk model using conformal transformation. [animation] |
|
Hyperbolic metric in the band model is given by: `(2/\pi)|dz|/ cos(Im(z))` [Hubbard J. - Teichmüller Theory.] At the center line of the band $|Im(z)| = 0$ the metric is euclidean. X-translation of the hyperbolic plane is simple euclidean translation. [animation] |
|
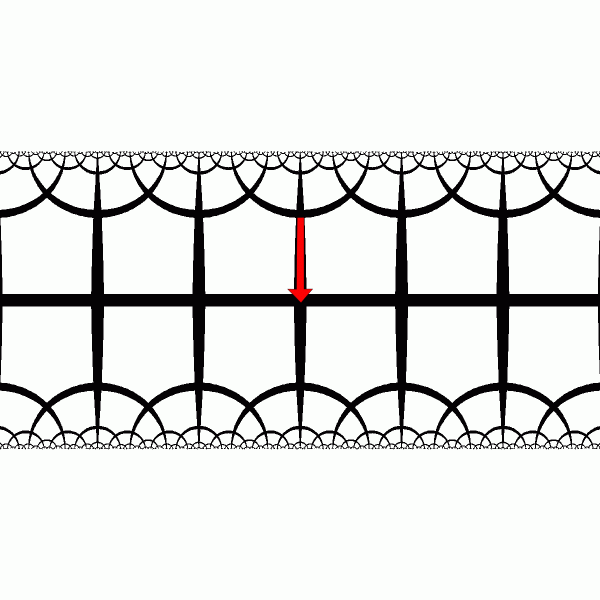
Y - translation looks more complex.
[animation] |
|
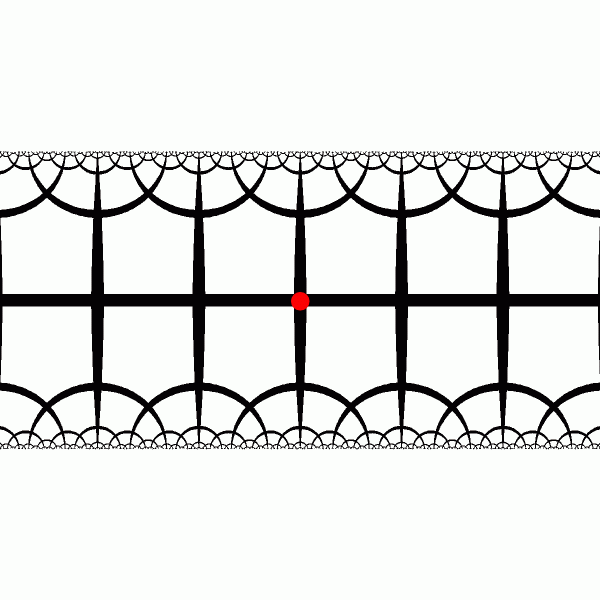
Rotation in band model looks very accelerated at the ends of the band
[animation] |
|
Ideal rotation around a point at $-\infty$ significanly moves only right half of the band.
[animation] |
|
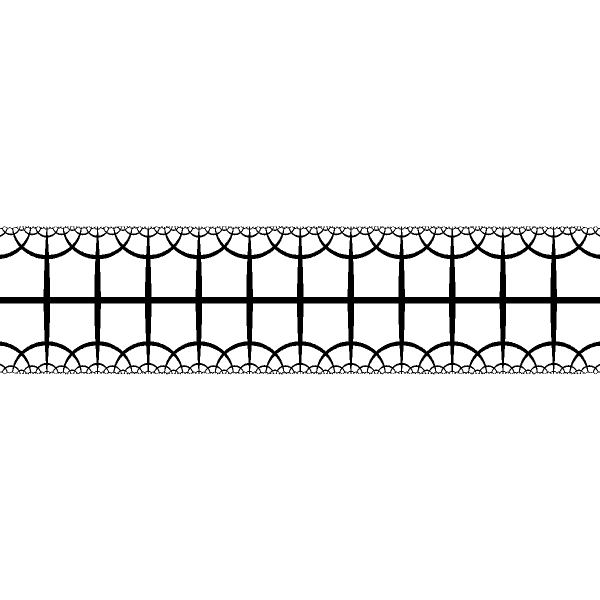
The hyperbolic tiling in the band model is periodic in R2. Is this coincidence? |
|
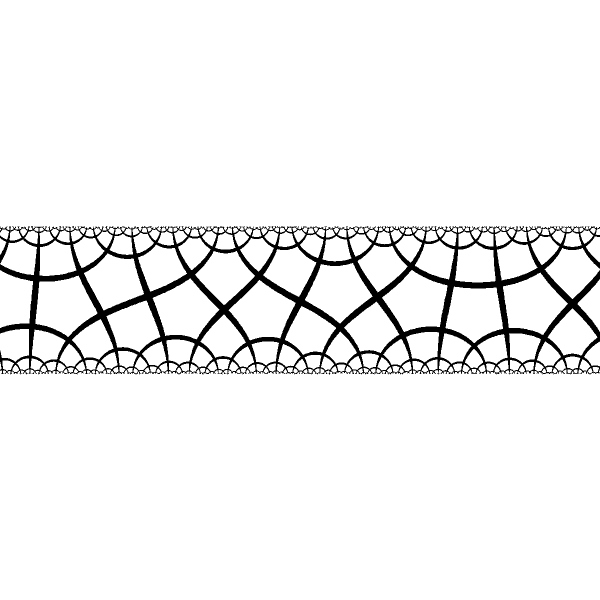
In the general case the tilng will not be peiodical in R2. In this case no period is visible. |
|
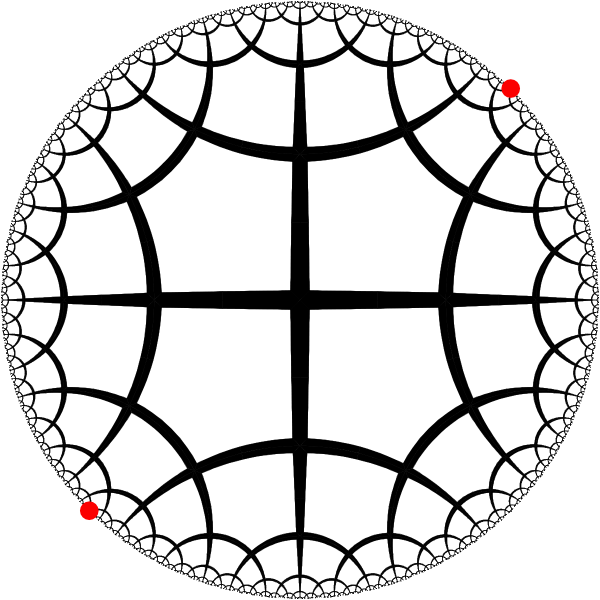
Symmetry transformations of the hyperbolic tiling are isometries of the hyperbolic plane. Isometries of the disk model are Moebius transformations with one or 2 fixed points. Transfomations with a pair of fixed points on the boundary of the unit disk correspond to some translation. |
|
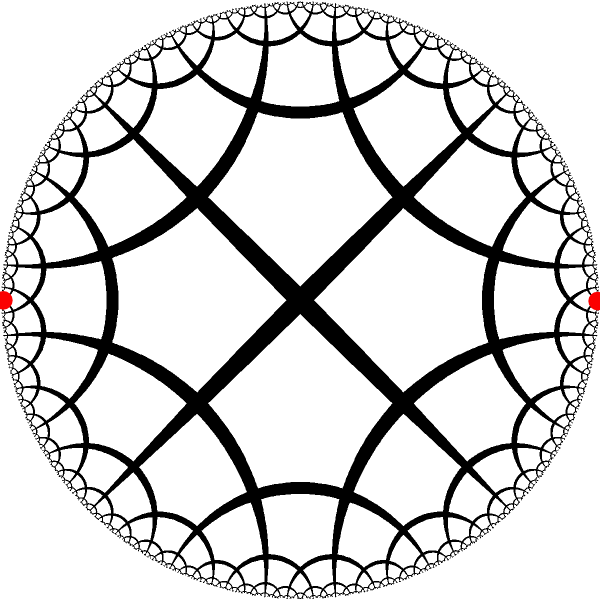
We can use isometry of H2 to move the pair of selected fixed points into the canonical positions $-1$ and $1$ |
|
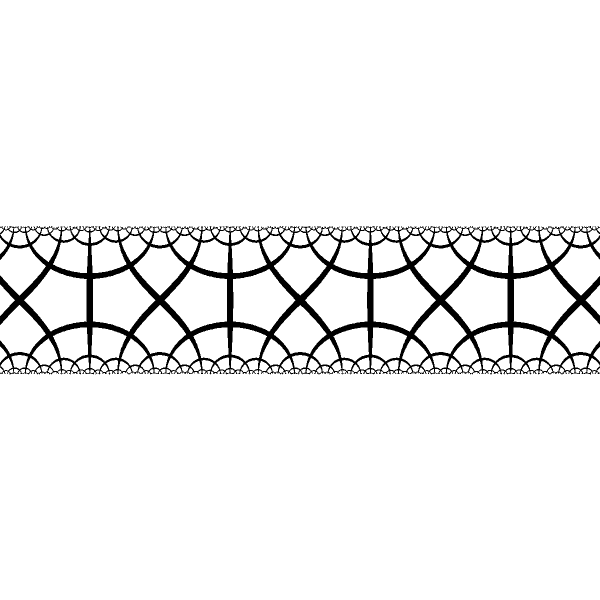
After applying `tanh^-1` transformation to the disk we have the band.
The tiling now is periodic, though its period is different and it looks differently.
|
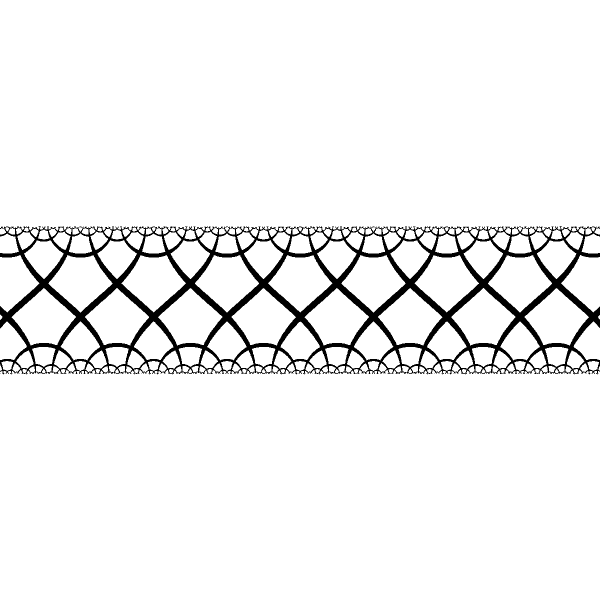
| Period varies for different pairs of fixed points. |
| Period varies for different pairs of fixed points. |
| Period varies for different pairs of fixed points. |
|
| Period varies for different pairs of fixed points. |
| Period varies for different pairs of fixed points. |
| Period varies for different pairs of fixed points. |
| Period varies for different pairs of fixed points. |
| Period varies for different pairs of fixed points. |
| Period varies for different pairs of fixed points. |
| Period varies for different pairs of fixed points. |
| Period varies for different pairs of fixed points. |
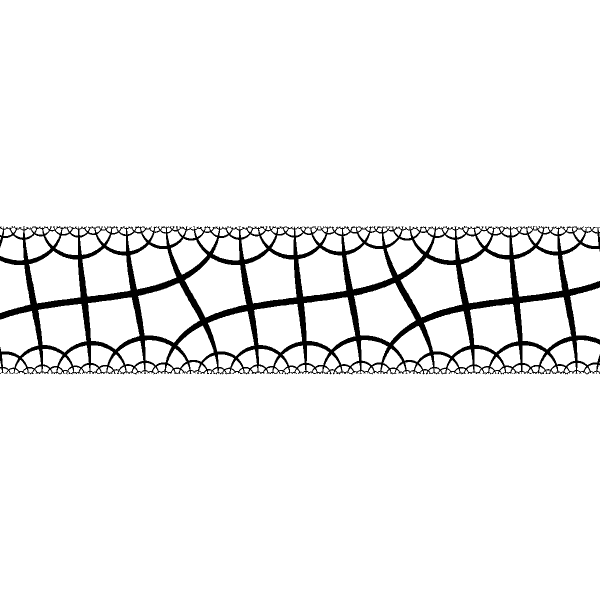
| Period varies for different pairs of fixed points. |
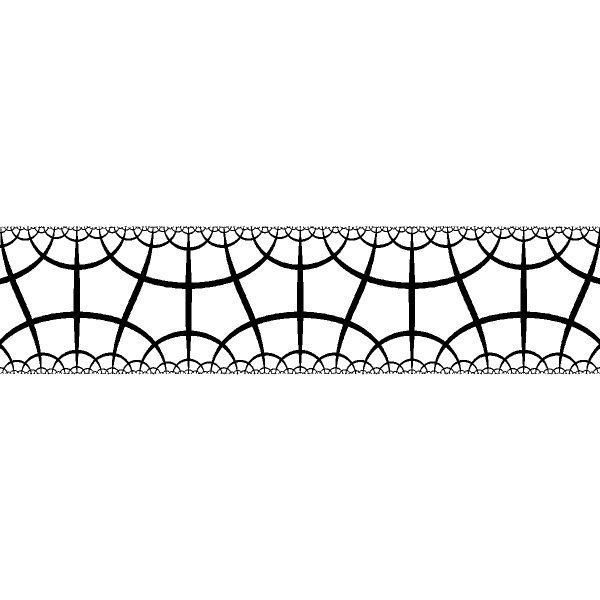
| Period varies for different pairs of fixed points. |
|
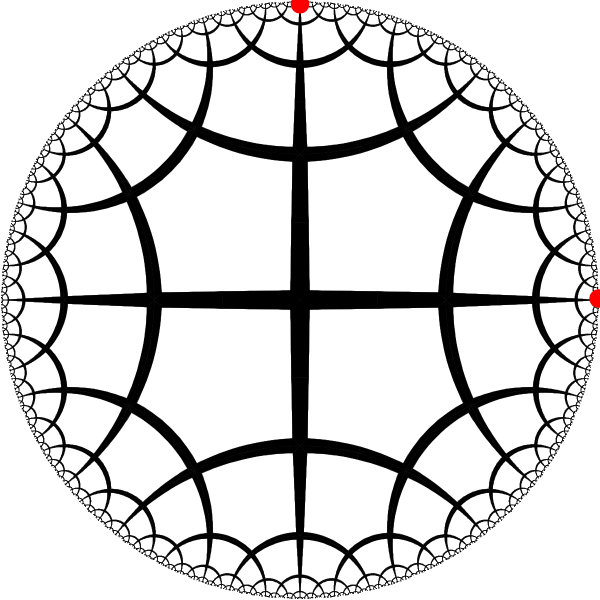
We can mix fixed points belonginh to the different isometries |
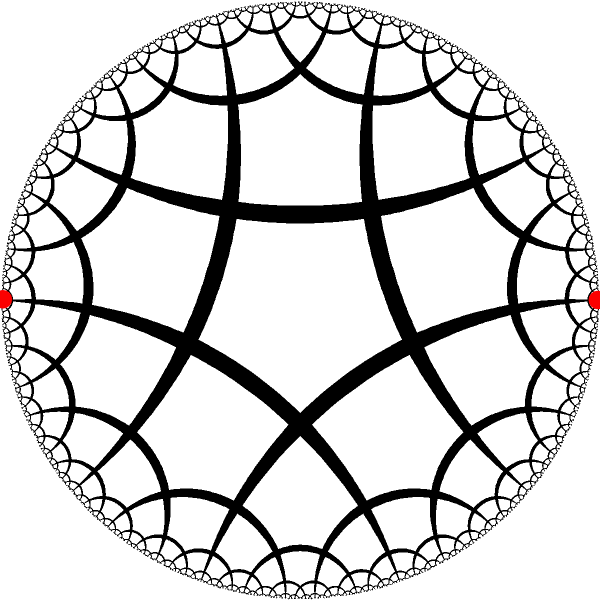
| We move fixed points into the canonical position: `-1, +1` |
|
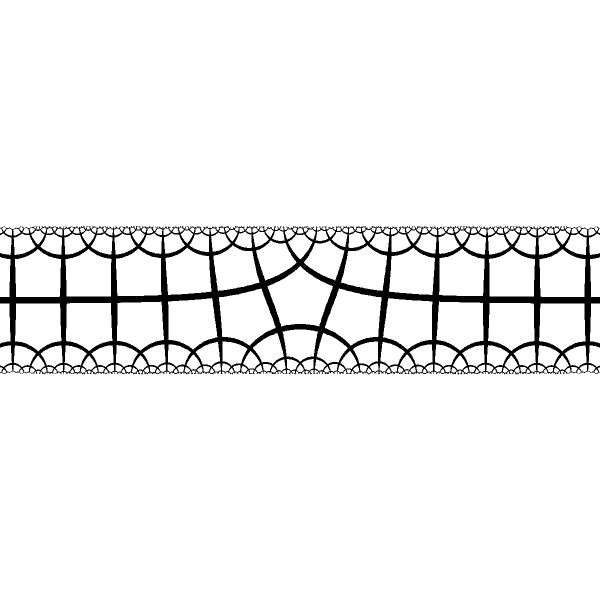
We stretch the disk into the band. When fixed points are of the same type, both ends of the band have the same asymptotic bevaviour and we have smooth transition between these asymptotes in the center |
|
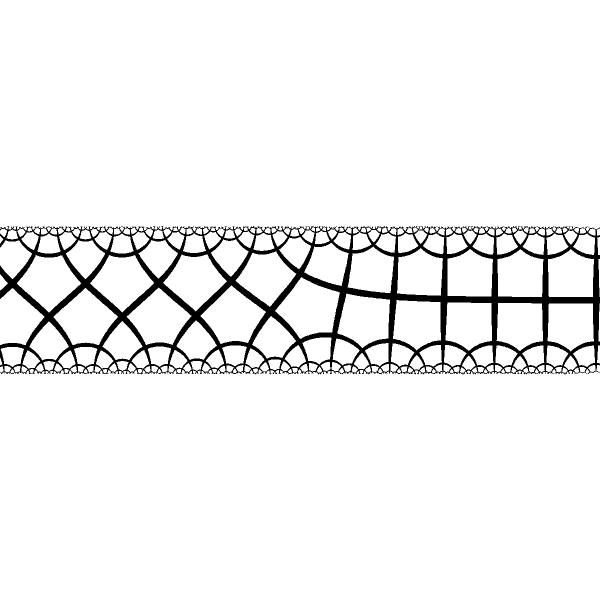
When fixed points are of the different type we have different periodical structures at the ends and smooth transition at the center |
|
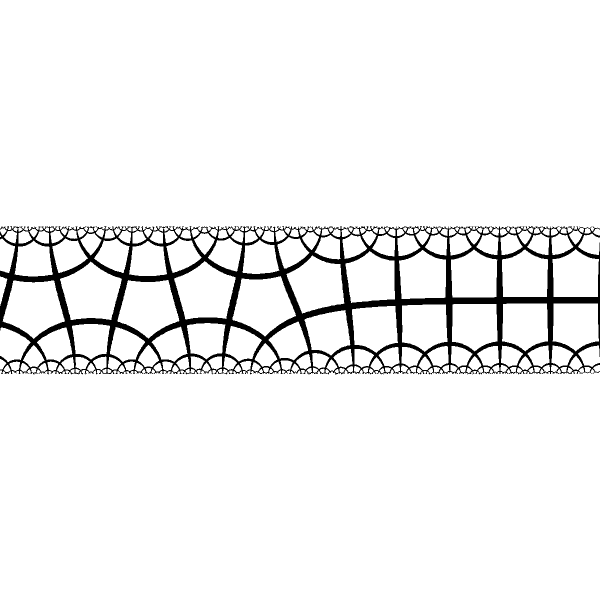
When fixed points are of the different type we have different periodical structures at the ends and smooth transition at the center |
|
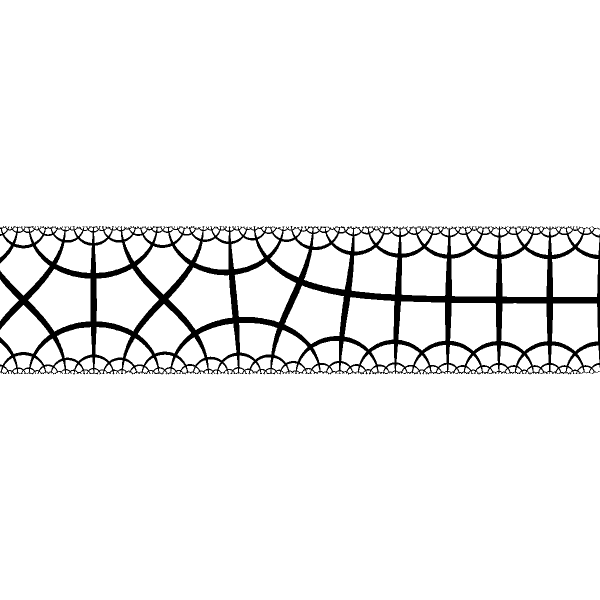
When fixed points are of the different type we have different periodical structures at the ends and smooth transition at the center |
|
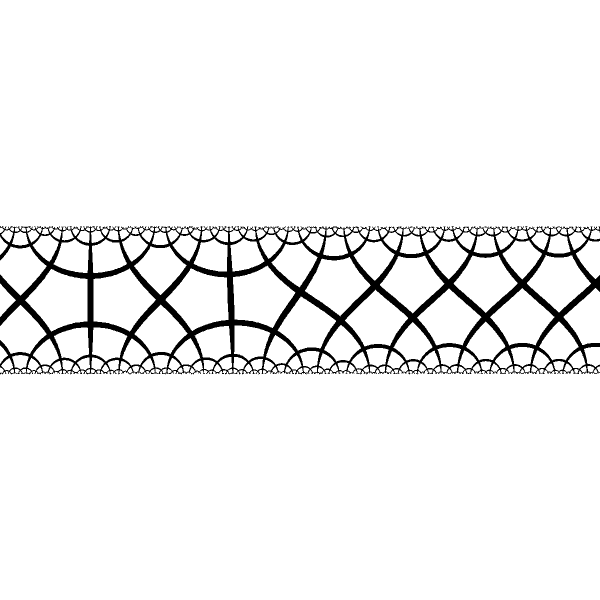
When fixed points are of the different type we have different periodical structures at the ends and smooth transition at the center |
|
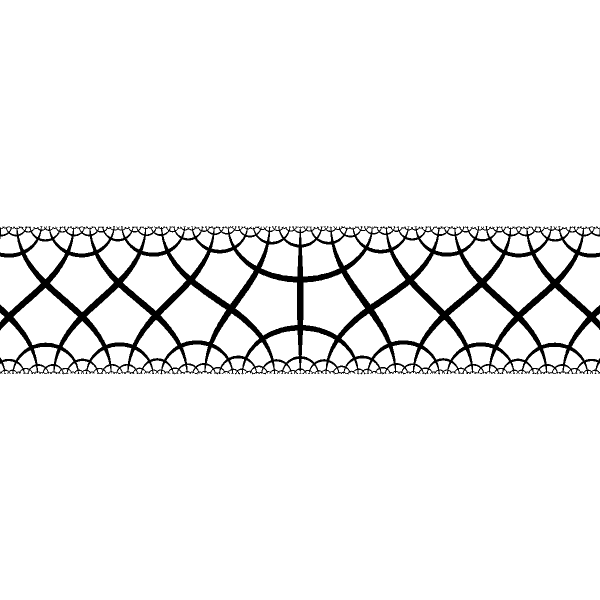
When fixed points are of the different type we have different periodical structures at the ends and smooth transition at the center |
|
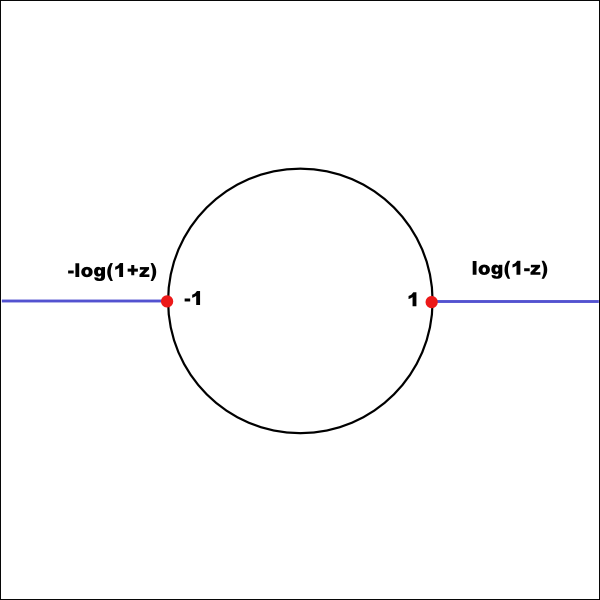
Proper way to calculate mapping by `tanh^-1` on complex plane is to use linear combination of `log()` `tanh^-1(z)=(1/2)(\log(1+z)-\log(1-z))` The map has 2 branching points with 2 cuts going from points -1 and 1 at the unit circle to `\infty` |
|
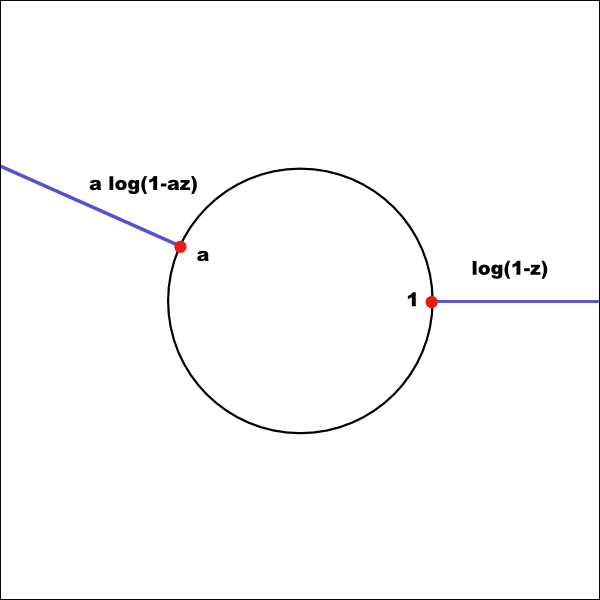
We can move one of the points and the corresponding cut anywhere we want by the following
simple modification of the mapping
`w = (1/2)(-a \log(1-az)-\log(1-z))`
This will make a Bended Band Model of the hyperbolic plane. [animation] of the mapping with moving point `a` on the unit circle |
|
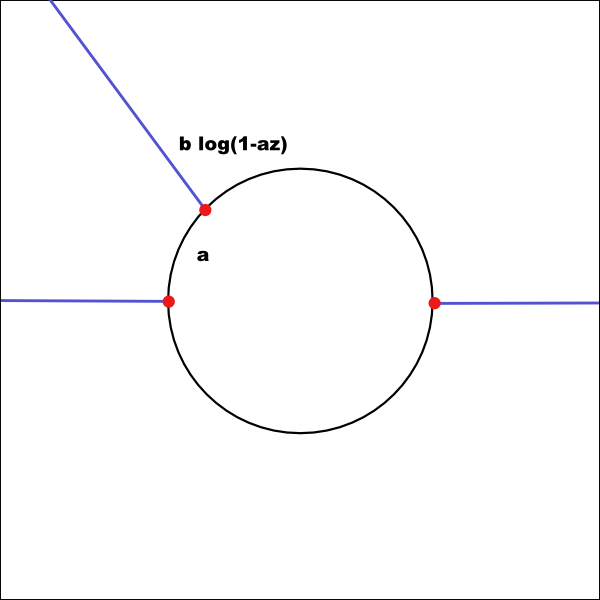
We may have arbitrary number of arms placed at some arbitrary locations `w = \sum_{i} b_i \log(1-a_i z)` During calculation we have to be carefull about the locations of the cuts and take apropriate branch of the `log` function. |
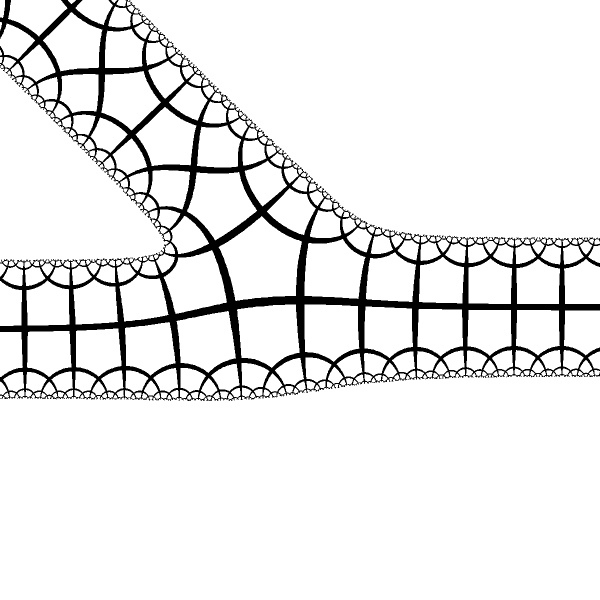
| Mapping with 3 arms. Two arms are located at the fixed poits of the same type, third arm is at the fixed point of different type. |
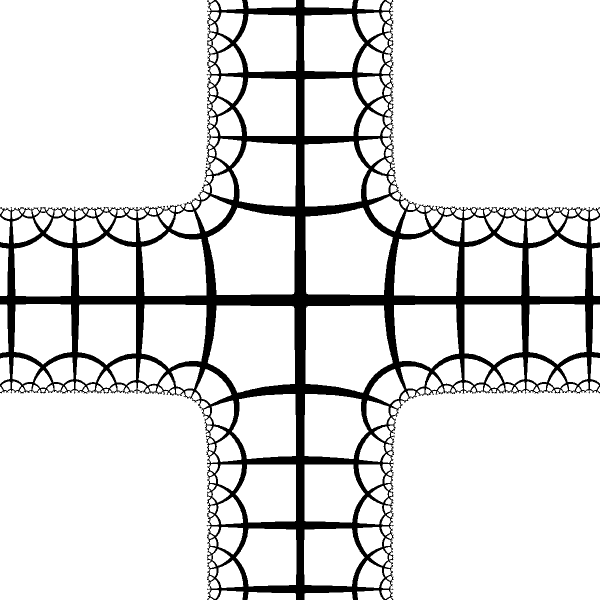
| Mapping with 4 arms. All arms originate from the fixed points of the same type. Therefore the arms have the same euclidean asymptotic behaviour. |
| Mapping with 4 arms. All 4 fixed point have the same type, but different from the above. |
| Another 4 arms mapping. |
| Mapping with 8 identical arms. |
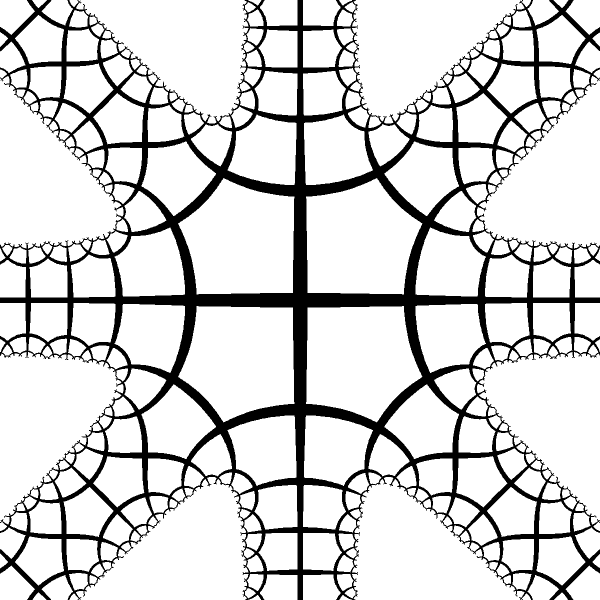
| Mapping with 8 arms of different type. |
|
We move origin of the hyperbolic plane into the center of pentagonal tile.
Now we have 5 symmetrical arms of the same type as in 4 arms case before.
|
|
Another comparision of 5 and 4 arms stars
|
|
Another comparision of 5 and 4 arms stars
|
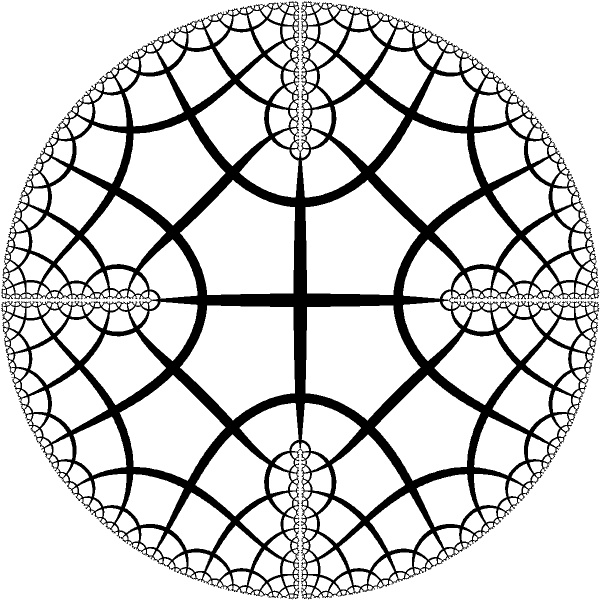
| Disk with 4 symmetrical cuts [animaton] of hyperbolic isometry in this model. |
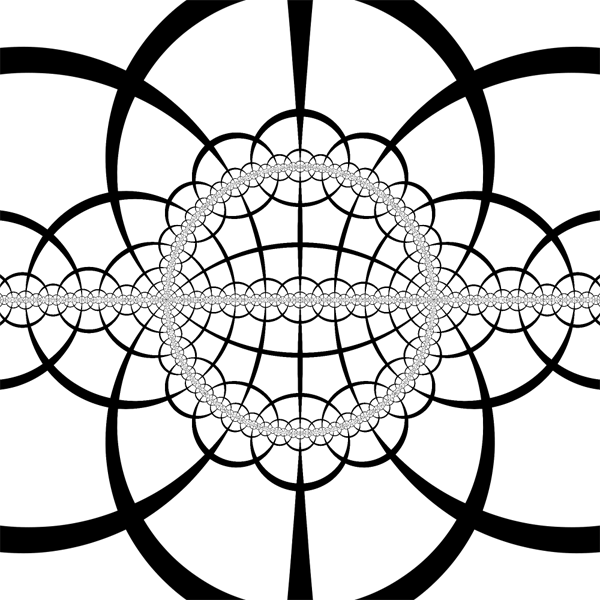
| Disk is mapped to half disk and 3 reflections in its sides are added |
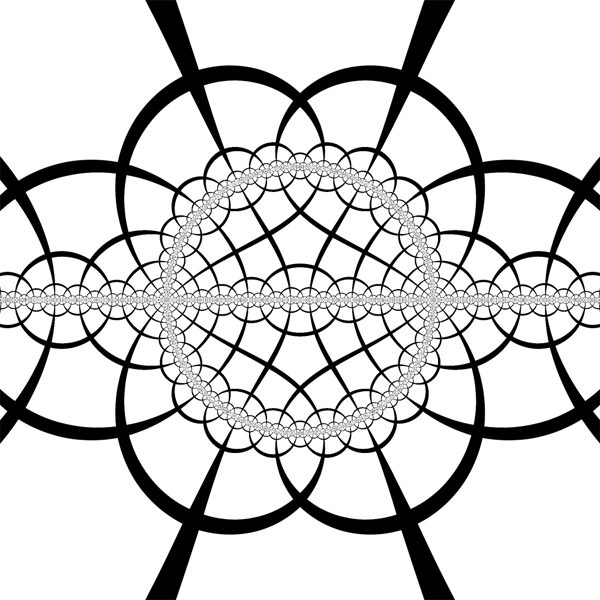
| Hyperbolic disk model is translated, disk is mapped to half disk and 3 reflections in its sides are added. |
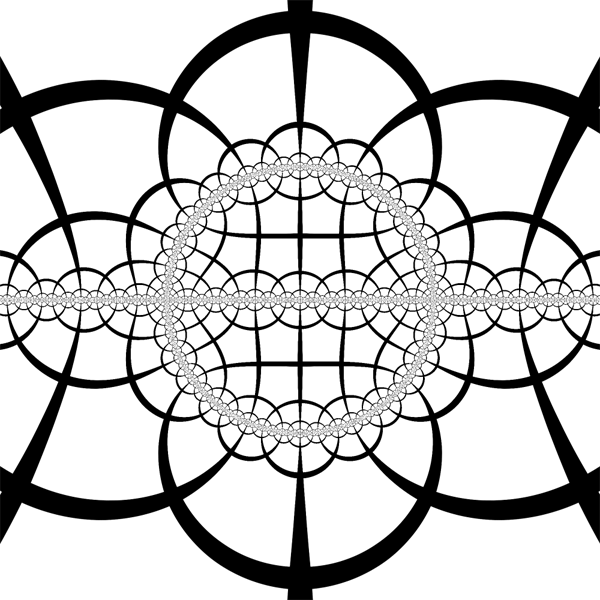
| Hyperbolic disk model is translated, disk is mapped to half disk and 3 reflections in its sides are added. |
|
Poincare disk is mapped to outside of the unit disk. Outside of the unit disk is mapped to
the outside of the Julia set of quadratic map `z \to z^2+c`. [animation] of the hyperbolic motion in the Julia or Fractal model of the hyperbolic plane |
| A `443` pattern in the hyperbolic plane in the disk model |
| The same patterns in the band model. One curve became straight line. This mean, that all the curves of this tiling are in fact equidistant lines. |
| Another view of the same patterns |
| Yet another view of the same pattern |
| The last view of the same pattern |
| `23x` tiling with 2 colors in the disk model |
| The same `23x` tiling with 2 colors in the band model |
| Another view of the same `23x` tiling |
| Last view of the same `23x` tiling |
| `4\star 3` Tiling of the sector. |
| Tiling of the disk with one cut. It is a sector with angle `360^o` - not the same as the unit disk. |
|
Tiling of the a ring.
Ring can be obtained from the band model using `w = exp(z/a)` with appropriate `a \in R` to make mapping periodic around the ring. |
| Some polynomial mapping of the disk. May be I will convert it into a piece of jewelry someday. |
| Mapping of the disk onto (almost) polygonal area |
| I have no idea how I've got this. |
| `23x` tiling of star with with 6 identical arms |
|
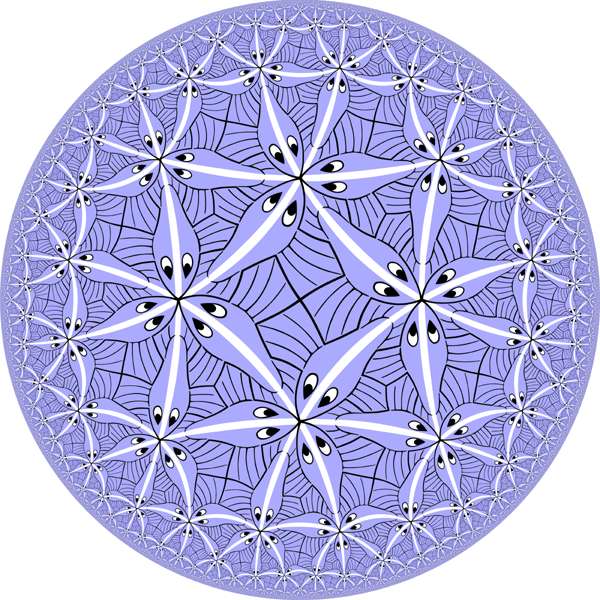
Tiling of Poicare circle derived from M.C.Escher "Circle Limit III"
Escher have made it without math and computer. Only compas, straight edge and steady hand. Amazing! |
The same tiling in the band model
|
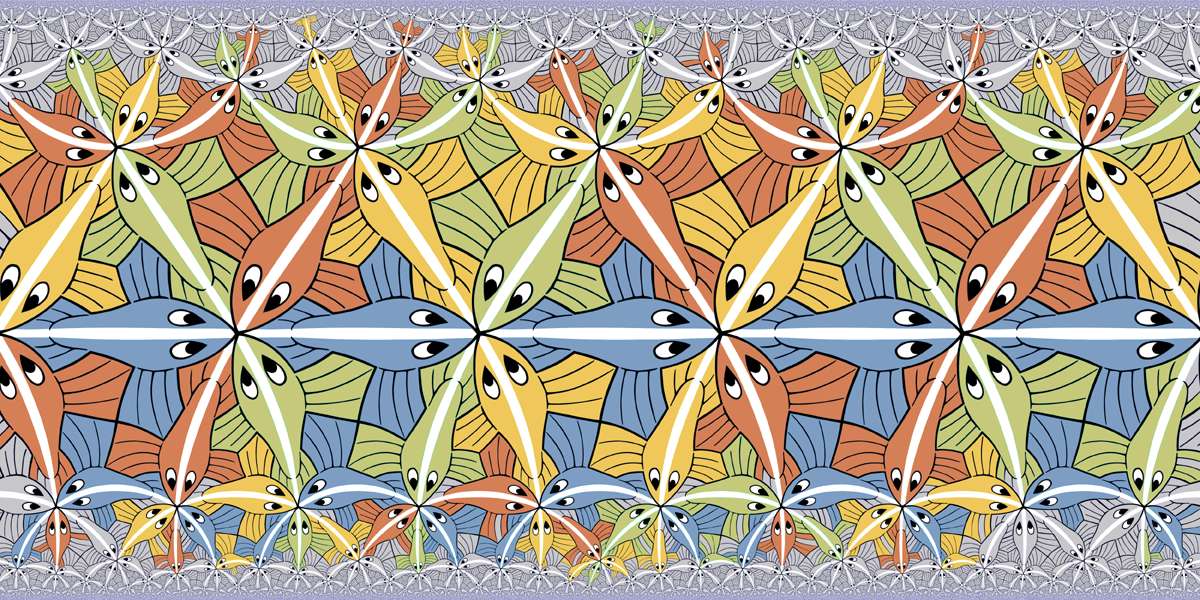The same tiling colored with 4 colors
|
Another version of the colored tiling
|
|
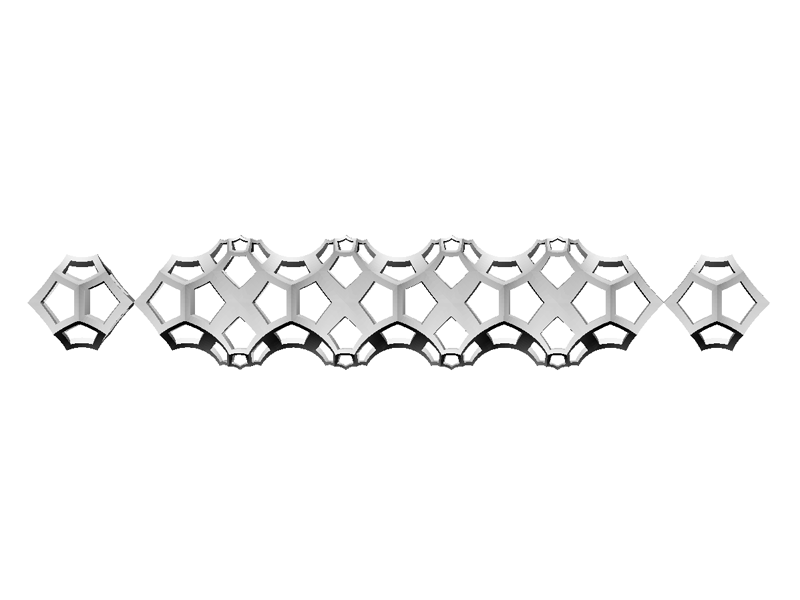
Straightforward generalization of the `log(1-z)` mapping to 3D will transform Poincare ball
into an infinite cylinder. It can be called Cylinder Model of H3.
Here we have tiling of H3 with right angled dodecahedra (only central chain is shown). Cylinder model is not conformal, but quasi conformal with anisotropy factor close to 1 (`\pi/2`?) Multi armed 3D stars are also possible. |